Prediction Market Prices != Probabilities
Context is that which is scarce
One of the most alluring things pro-prediction market people say to skeptics is, "If the price is incorrect, you can fix it and make money doing so!"
Polymarket's own website states this equivalent as fact:
Prices = Probabilities.
Prices (odds) on Polymarket represent the current probability of an event occurring. For example, in a market predicting whether the Miami Heat will win the 2025 NBA Finals, if YES shares are trading at 18 cents, it indicates a 18% chance of Miami winning.
These odds are determined by what price other Polymarket users are currently willing to buy & sell those shares at. Just how stock exchanges don't "set" the prices of stocks, Polymarket does not set prices / odds, they're a function of supply & demand.
The logic mirrors the question posed to market bears who performatively claim asset prices are overvalued: "Are you short?" Here is a liquid venue to express your view and profit if you're right. When asked, most aren't actually short.
Last year, Dan Robinson posted a theoretical question about prediction markets in an X poll, asking what the price of a prediction market would trade at, given a known probability of an event occurring:
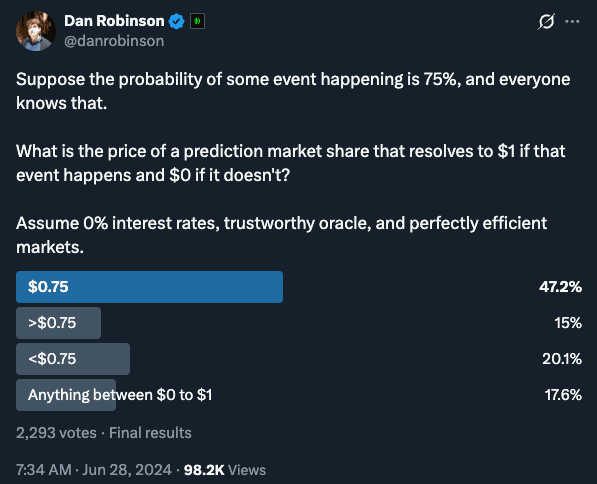
According to Dan, only 403 out of 2,293 people answered this correctly.
Stop here to think about it before scrolling down for Dan's solution.
Dan's solution
If the title didn't already give it away, it is not the most popular answer: $0.75 (A).
Dan claims that the answer is D: Anything between $0 to $1. His rationale is as follows:
- Prediction market payouts are denominated in a base currency such as USD. Users use USD to buy contracts and are paid out in USD if the market resolves in their favor.
- Some prediction markets result in changing the value of the underlying base currency on a per unit basis.
- Traders engage with prediction markets with full context on the value of the base currency with respect to its ability to purchase goods and services, not in a dollar for dollar vacuum.
- This means that the different outcomes prices do not necessarily correspond to respective probabilities but rather the average of every trader's utility function in those two cases.
So a market that asks, "Will the US exist in 5 years?" will not have prices that reflect the actual probability that people believe. Instead, each outcome will trade at the following:
- YES: $1
- NO: $0
NO shares should trade at $0 because if the US does not exist in 5 years the dollar is worthless. So nobody would rationally pay any money for a NO share today because the payout in the case that they are correct would give them no benefit.
Note that this creates some technical edge cases (outside of Dan's original line of questioning). If the market is on Polymarket, USDC is the numeraire. The market should account for scenarios where the US collapses but USDC retains value through social consensus (low probability, but non-zero). In that case, NO shares might trade slightly above $0.
In the furthest extreme where a question instead asks, "Will humanity exist in 5 years?" Money is completely worthless in the NO outcome, so that market should trade at exactly $1 for YES and $0 for NO, regardless of extinction risk.
Context is that which is scarce, especially in prediction markets.
Back to reality
The natural objection is that this is a clever thought experiment but doesn't matter in practice. Real prediction markets ask questions where the currency retains value regardless of outcome.
I would then point you to the Jesus Christ market, and, yes, this is a real market:
The value of the dollar in the case of Jesus Christ returning is an exercise left to the reader.
But even for serious markets, there are cases where prices diverge from probabilities.
The US presidential election is one example. "Will Trump win the US presidential election?" (very likely) did not trade at pure probabilities.
If you believe Trump's policies would weaken the dollar (higher inflation, tariffs, fiscal expansion), then a Trump win means your payout is worth less in real terms. The market price in that scenario would reflect:
Trump winning = X * (purchasing power of $1 under Trump)
Trump losing = (1 - X) * (purchasing power of $1 under Harris)
Just looking at the Polymarket homepage suggests that there are quite a few markets where this logic might apply:
Misc. Thoughts
- Can we quantify the numeraire distortion in real money markets today for a specific market?
- How many markets should one expect this to apply to?
- Play money markets perform extremely well relative to what one might expect given the lack of economic incentives. How much can be attributed to numeraire effects, selection effects, or some other factor?
Popularity prediction hash: 65797d0398c456f539a32c1c156b2d7e69850209f2da544d14c2bb3babae6d6a